Next Permutation
題意:給定一排列,找出它的下一個
解題思路:
一開始也不知怎作,但網上有個演算法如下:
- 由後往前找到第一個 $$i$$ ,使得
A[i] < A[i+1] - 從陣最最後一位一直搜尋到 $$i+1$$ ,找出一個 $$j$$ ,使得
A[j] > A[i],將兩者交換 - 接著將 pivot 後半段作反轉。
網友 水中的魚 提供了下面精美的圖:
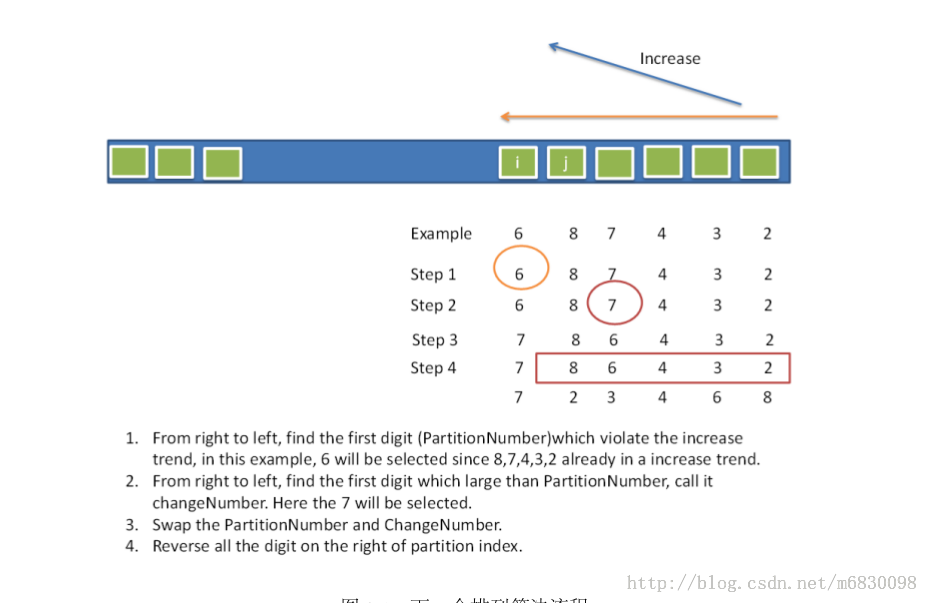
引用 網友neverlandly 清楚的解說:
用一個例子來說明,比如排列是(2,3,6,5,4,1),求下一個排列的基本步驟是這樣:
1) 先從後往前找到第一個不是依次增長的數,記錄下位置p。比如例子中的3,對應的位置是1;
2) 接下來分兩種情況:
1. 如果上面的數字都是依次增長的,那麼說明這是最後一個排列,下一個就是第一個,其實把所有數字反轉過來即可(比如(6,5,4,3,2,1)下一個是(1,2,3,4,5,6));
2 否則,如果p存在,從p開始往後找,找到下一個數就比p對應的數小的數字,然後兩個調換位置,比如例子中的4。調換位置後得到(2,4,6,5,3,1)。最後把p之後的所有數字倒序,比如例子中得到(2,4,1,3,5,6), 這個即是要求的下一個排列。
以上方法中,最壞情況需要掃瞄數組三次,所以時間複雜度是O(3*n)=O(n),空間複雜度是O(1)。
程式碼如下:
public class Solution {
/**
* @param nums: an array of integers
* @return: return nothing (void), do not return anything, modify nums in-place instead
*/
public int[] nextPermutation(int[] nums) {
if (nums == null || nums.length < 2) {
return nums;
}
int len = nums.length;
int pivot = -1;
for (int i = len - 2; i >= 0; i--) {
if (nums[i] < nums[i + 1]) {
pivot = i;
break;
}
}
// 這題難在如何處理邊際條件
// 如果pivot等於-1的話,代表目前的排列為降序,且是最後一個排列,
// 若不等於-1,則代表pivot右邊至少存在一數比pivot大,找到它並與pivot交換
// 此作法是把pivot的右側調整為降序
if (pivot != -1) {
for (int i = len - 1; i > pivot; i--) {
if (nums[i] > nums[pivot]) {
swap(nums, i, pivot);
break;
}
}
}
// 把pivot的右邊作翻轉(即排成升序)即可,因pivot的右邊為降序
reverse(nums, pivot + 1, len - 1);
return nums;
}
private void swap (int[] A, int a, int b) {
int temp = A[a];
A[a] = A[b];
A[b] = temp;
}
private void reverse(int[] A, int start, int end) {
while (start < end) {
int temp = A[start];
A[start] = A[end];
A[end] = temp;
start++;
end--;
}
}
}
updated 2015.11.18
public class Solution {
public void nextPermutation(int[] nums) {
if (nums == null || nums.length < 2) {
return;
}
int pos = -1;
int len = nums.length;
for (int i = len - 2; i >= 0; i--) {
if (nums[i] < nums[i + 1]) {
pos = i;
break;
}
}
if (pos == -1) {
reverse(nums, 0, len -1);
return;
}
int k = len - 1;
for (; k > pos; k--) {
if (nums[pos] < nums[k]) {
break;
}
}
swap(nums, pos, k);
reverse(nums, pos + 1, len - 1);
}
private void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
private void reverse(int[] nums, int start, int end) {
while (start < end) {
swap(nums, start, end);
start++;
end--;
}
}
}
Time Complexity:$$O(N)$$